Contenuti:
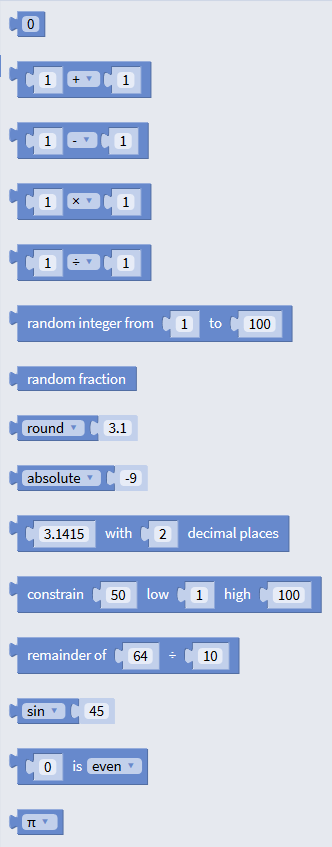
- 0 (basic number block)
- 0 (radix number block)
- = Uguale a
- ≠ Diverso da
- > Maggiore di
- ≥ Maggiore o uguale a
- < Minore di
- ≤ Minore o uguale a
- + Addizione
- – Sottrazione
- * Moltiplicazione
- / Divisione
- ^ Elevazione a potenza (#exponent)
- random integer
- random fraction
- random set seed to
- min
- max
- sqrt
- abs
- neg
- log
- e^
- round
- ceiling
- floor
- modulo
- remainder
- quotient
- sin
- cos
- tan
- asin
- acos
- atan
- atan2
- convert radians to degrees
- convert degrees to radians
- format as a decimal
- is a number?
- convert number
- bitwise and
- bitwise or (inclusive)
- bitwise or (exclusive)
| App Inventor 2 | Kodular | ThunkableX |
|---|---|---|
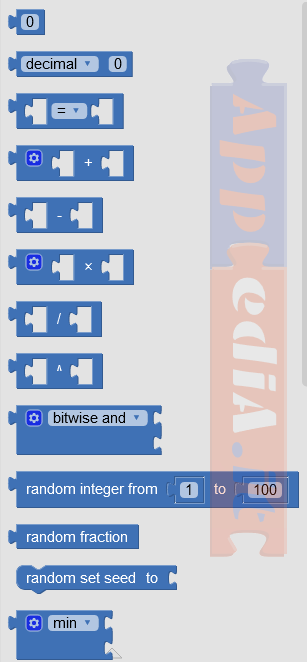 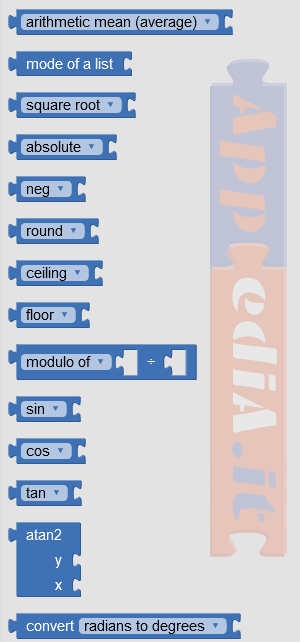  |
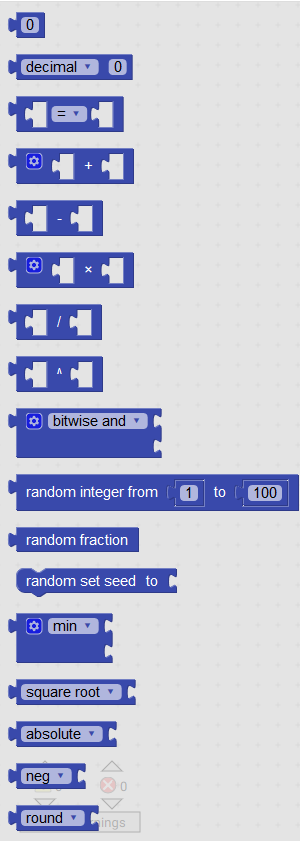  |
 |

L’ordine delle operazioni
Ordine delle operazioni (PEMDAS):
- Fai prima ciò che è tra parentesi. (P)
- Valuta gli esponenti. (E)
- Moltiplicazioni o divisioni hanno la precedenza su addizioni e sottrazioni. (MDAS)
- Lavora da sinistra a destra.
Esempi
4 + 6 – 2 = (4 + 6) – 2 = 10 – 2 = 8 ; Da sinistra a destra poiché gli operatori hanno la stessa precedenza:

4 * 6 – 2 = (4 * 6) – 2 = 24 – 2 = 22 ; MD prima di AS:
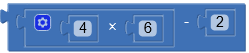
4 + 2 * 6 = 4 + (2 * 6) = 4 + 12 = 16 ; MD prima di AS:

Le parentesi possono sovrascrivere il normale “MD prima di AS” come in questo esempio (non ci sono parentesi ma una loro emulazione, dovuta all’ordine dei blocchi) :
4 * (6 + 2) = 4 * 8 = 32 ; P prima di MD

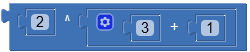
2 ^ 3 + 1 = (2 ^ 3) + 1 = 8 + 1 = 9 ; E prima di AS

A volte gli esponenti sono tra parentesi:
2 ^ (3 + 1) = 2 ^ 4 = 16 ; P prima di E
Radici quadrate e diverse parentesi:
sqrt((x2 – x1) ^ 2 + (y2 – y1) ^ 2)
![]()
Blocco numerico Radix
Rappresenta un numero di base 10. Cliccando su “0” ti permetterà di cambiare il numero. Facendo clic sul menu a discesa, potrai inserire un numero in una base numerica diversa (anche conosciuto come radix). Il numero sarà quindi “tradotto” in decimale (base-10). Ad esempio, questi tre blocchi sono equivalenti:= {# =} Uguale a
Verifica se due numeri sono uguali e restituiscevero o falso.
≠ {# not =} Diverso da
Verifica se due numeri non sono uguali e restituiscevero o falso.
< Minore di
Verifica se il primo numero è inferiore al secondo e restituiscevero o falso.
≤ Minore o uguale a
Verifica se il primo numero è inferiore o uguale al secondo numero e restituiscevero o falso.
+ Addizione
Restituisce il risultato della somma di qualsiasi quantità di blocchi che hanno un valore numerico insieme. I blocchi con un valore numerico includono il blocco numerico di base, la lunghezza dell’elenco o del testo, le variabili con un valore numerico, ecc. Questo blocco è un mutatore e può essere espanso per consentire più numeri nella somma.– Sottrazione
Restituisce il risultato della sottrazione.* Moltiplicazione
Restituisce il risultato della moltiplicazione di qualsiasi quantità di blocchi che hanno un valore numerico insieme. È un blocco mutatore e può essere espanso per consentire più numeri nel prodotto.^ Elevazione a potenza
Restituisce il risultato del primo numero elevato alla potenza del secondo.random integer
Restituisce un valore intero casuale tra i valori indicati, incluso. L’ordine degli argomenti non ha importanza.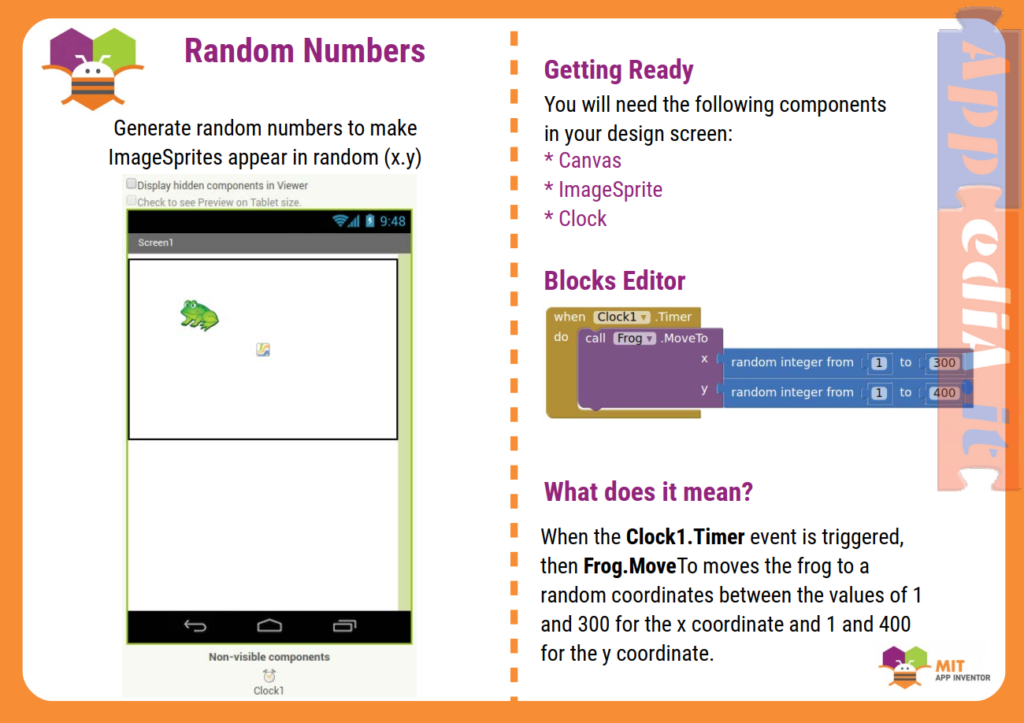
random fraction
Restituisce un valore casuale compreso tra 0 e 1.random set seed to
Utilizzare questo blocco per generare sequenze ripetibili di numeri casuali. È possibile generare la stessa sequenza di numeri casuali chiamando prima ilrandom set seed con lo stesso valore. Questo è utile per testare programmi che coinvolgono valori casuali.Un generatore di numeri pseudocasuali è un algoritmo per generare una sequenza di numeri che approssima le proprietà dei numeri casuali. Un seme casuale è un numero o un vettore scelto e utilizzato per inizializzare questo generatore di numeri. Scegliendo diversi semi casuali, il tuo algoritmo sceglierà numeri casuali in un modo leggermente diverso. La scelta di un seme univoco restituirà una sequenza di numeri casuali univoci.
Ciò significa che se utilizzi continuamente lo stesso seme e scegli un elemento casuale per una grande quantità di test e dati, non otterrai risultati così diversi o veramente casuali come se scegliessi un nuovo seme ogni volta.
min
Restituisce il valore più piccolo di un insieme di numeri. Se ci sono prese scollegate nel blocco, min considererà anche 0 nella sua serie di numeri. Questo blocco è un mutatore e un menu a discesa.max
Restituisce il valore più grande di un insieme di numeri. Se nel blocco sono presenti prese scollegate, max considererà anche 0 nella sua serie di numeri. Questo blocco è un mutatore e un menu a discesa.sqrt
Restituisce la radice quadrata del numero indicato.abs
Restituisce il valore assoluto di un determinato numero. Ad esempio il valore assoluto di -5 è 5. Il valore assoluto di +7 è 7. Il valore assoluto di -3/2 è 3/2. E così via per qualsiasi numero reale.- una successione di cifre (cioè simboli 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9),
- una virgola (ad esempio 12,3456)
- un segno (– oppure +, e quest’ultimo in genere non si scrive esplicitamente).
Esempi di numeri reali sono -9 (”meno nove”) oppure 12,345 (”dodici virgola tre quattro cinque”) e numeri la cui rappresentazione decimale non ha termine (periodici).
neg
Restituisce il negativo di un determinato numero.
log
Restituisce il logaritmo naturale di un dato numero, ovvero il logaritmo alla base e (2.71828…).
e ^
Restituisce e (2.71828…) elevato alla potenza di un determinato numero.
round Arrotondamento
Partendo da un numero con virgola, restituisce il numero dato arrotondato al numero intero più vicino (in funzione della parte frazionaria).
- Se la parte frazionaria è <0.5 verrà arrotondata per difetto. Round 3,1=3
- Se la parte frazionaria è >0.5 sarà arrotondato per eccesso. Round 3,6=4
- Se è esattamente uguale a 0.5,
- i numeri con una parte intera pari saranno arrotondati per difetto (4,5 in 4)
- i numeri con una parte intera dispari saranno arrotondati per eccesso. (3,5 in 4). (Questo metodo è chiamato round to even cioè arrotondamento al pari)
Divertiti con la mia applicazione dedicata agli arrotondamenti
Scarica il file in formato .APK e installa l’App sul tuo Smartphone: ARROTONDA
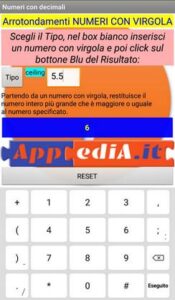
ceiling (funzione Parte intera superiore)
(Ceiling in Inglese significa Soffitto) Partendo da un numero con virgola, restituisce il numero intero più grande che è maggiore o uguale al numero specificato.
Esempio: Ceiling 3,5=4; Ceiling 3,1=4 ; Ceiling 3,6=4
Divertiti con la mia applicazione dedicata agli arrotondamenti
Scarica il file in formato .APK e installa l’App sul tuo Smartphone: ARROTONDA

floor (funzione parte intera inferiore)
(Ceiling in Inglese significa Pavimento) Partendo da un numero con virgola, restituisce il numero intero più piccolo che è minore o uguale al numero dato. Insomma, è la funzione che associa ad ogni numero reale il più grande intero minore o uguale a .
Esempio: Floor 3,5=3; Floor 3,1=3 ; Floor 3,6=3
Divertiti con la mia applicazione dedicata agli arrotondamenti
Scarica il file in formato .APK e installa l’App sul tuo Smartphone: ARROTONDA

modulo
Modulo (a, b) è uguale al resto (a, b) quando a e b sono dello stesso segno, positivi o negativi. Precisamente il modulo è la distanza tra due numeri.Modulo (a, b) ha sempre lo stesso segno di b, mentre il resto (a, b) ha sempre lo stesso segno di a.
remainder
Il resto (a, b) restituisce il risultato della divisione di a per b e prende il resto. Il resto è la parte frazionaria del risultato moltiplicata per b.
Ad esempio, resto (11,5) = 1 perché 11/5 = 2.2 cioè l’intero 2, più il resto 0.2 (cioè 1 ⁄ 5). In questo caso, 1 ⁄ 5 è la parte frazionaria.
Moltiplichiamo 1/5 per b, cioè 5 e otteniamo 1, il resto.
Altri esempi sono resto (-11, 5) = -1, resto (11, -5) = 1 e resto (-11, -5) = -1.
quotient
Restituisce il quoziente, cioè il risultato della divisione del primo numero (dividendo) per il secondo (divisore) e dell’eliminazione di qualsiasi parte frazionaria del risultato.
sin
Restituisce il seno del numero dato in gradi.
cos
Restituisce il coseno del numero dato in gradi.
tan
Restituisce la tangente del numero dato in gradi.
asin
Restituisce l’ arcoseno del numero dato in gradi.
acos
Restituisce l’ arcocoseno del numero indicato in gradi.
atan
Restituisce l’ arcotangente del numero dato in gradi.
atan2
Restituisce l’arcotangente di y / x, dato yey x.
convert radians to degrees
Restituisce il valore in gradi del numero dato in radianti. Il risultato sarà un angolo nell’intervallo [0, 360)
convert degrees to radians
Restituisce il valore in radianti del numero dato in gradi. Il risultato sarà un angolo nell’intervallo [-π, + π)
format as decimal
Formatta un numero come un decimale con un determinato numero di posizioni (places) dopo la virgola decimale. Il numero di posti deve essere un numero intero non negativo. Il risultato viene prodotto arrotondando il numero (se c’erano troppi posti) o aggiungendo zeri a destra (se ce n’erano troppo pochi).
Ad esempio:
- i numeri 3.23111 o 3.23999 con posizioni = 1, danno sempre 3.2
- 3.23111 con posizioni = 2, dà 3.23
- 3.23999 con posizioni = 2, dà 3.24
- 3.23111 con posizioni = 3, dà 3.231
- 3.23999 con posizioni = 3, dà 3.240
- 3.23555 con posizioni = 2, dà 3.24
- 3.23555 con posizioni = 3, dà 3.236
Divertiti con la mia applicazione dedicata agli arrotondamenti
Scarica il file in formato .APK e installa l’App sul tuo Smartphone: ARROTONDA

is a number?
Restituisce vero se l’oggetto dato è un numero e falso altrimenti.
convert number
Accetta una stringa di testo che rappresenta un numero intero positivo in una base e restituisce una stringa che rappresenta lo stesso numero è un’altra base. Ad esempio, se la stringa di input è 10, la conversione dalla base 10 alla binaria, produrrà la stringa 1010; mentre se la stringa di input è la stessa 10, la conversione dalla binaria alla base 10 produrrà la stringa 2. Se la stringa di input è la stessa 10, la conversione dalla base 10 in esadecimale produrrà la stringa A.
Bitwise And
Prende due numeri e confronta ogni coppia di bit (bit per bit). Ogni bit del risultato è 1 solo se i bit corrispondenti di entrambi gli operandi sono 1. Esempio: 
Bitwise OR (Inclusive)
Prende due numeri e confronta ogni coppia di bit. Ogni bit del risultato è 1 se uno dei bit corrispondenti in ciascun operando è 1. Esempio: 
Bitwise Or (Exclusive)
Prende due numeri e confronta ogni coppia di bit. Ogni bit del risultato è 1 solo se un bit corrispondente negli operandi è 1 e l’altro è 0. Esempio: 
Blocchi matematici su liste
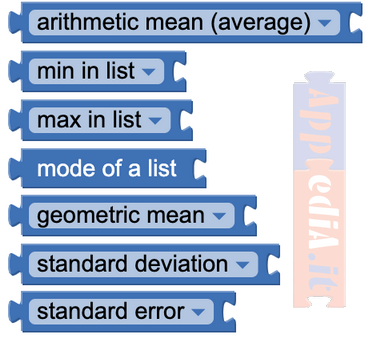
- Arithmetic Mean – Average (Calcola la media aritmetica degli elementi in una lista)
- Min in List (Restituisce l’elemento minimo in un elenco)
- Max in List (Restituisce l’elemento massimo in un elenco)
- Mode of a List (Restituisce l’elemento più frequente in un elenco)
- Geometric Mean (Calcola la media geometrica degli elementi in una lista)
- Standard deviation (Calcola le deviazioni standard (popolazione) degli elementi in un elenco)
- Standard error (Calcola l’errore standard degli elementi in un elenco)
| Aggiornato al 10/03/2023 | |
| Aggiornato al 01/05/2021 | |
| Aggiornato al 01/05/2021 |
PDF Lista comparazione dei componenti di AI2 KODULAR THUNKABLEX agg.20210911
Vuoi avere più informazioni sul Coding visuale? Vai alla pagina dei Blocchi incorporati dove potrai imparare a scrivere il linguaggio di programmazione per App Inventor 2, Kodular e Thunkable X. Visita la pagina del Blog con le ultime notizie sulle le tre piattaforme. Nella pagina Documentazione troverai i collegamenti ai forum, il glossario, i link ai siti dei migliori programmatori, i download e tanti altri accessori.

